グラフ問題 競プロ 899127

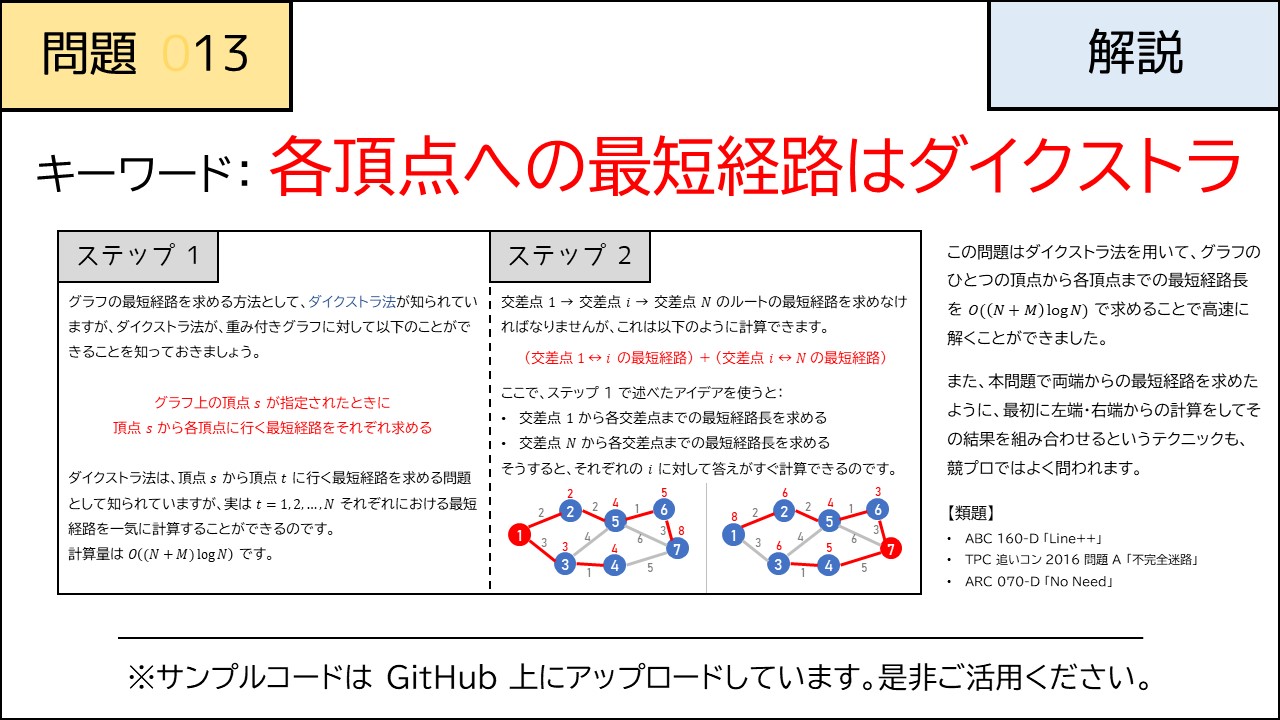
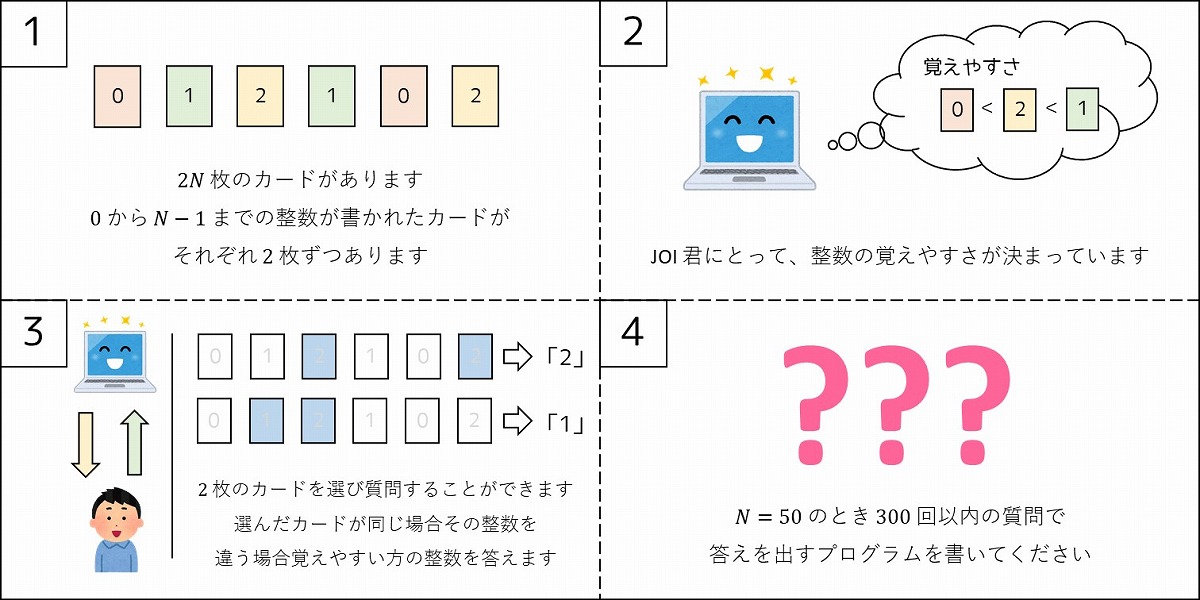
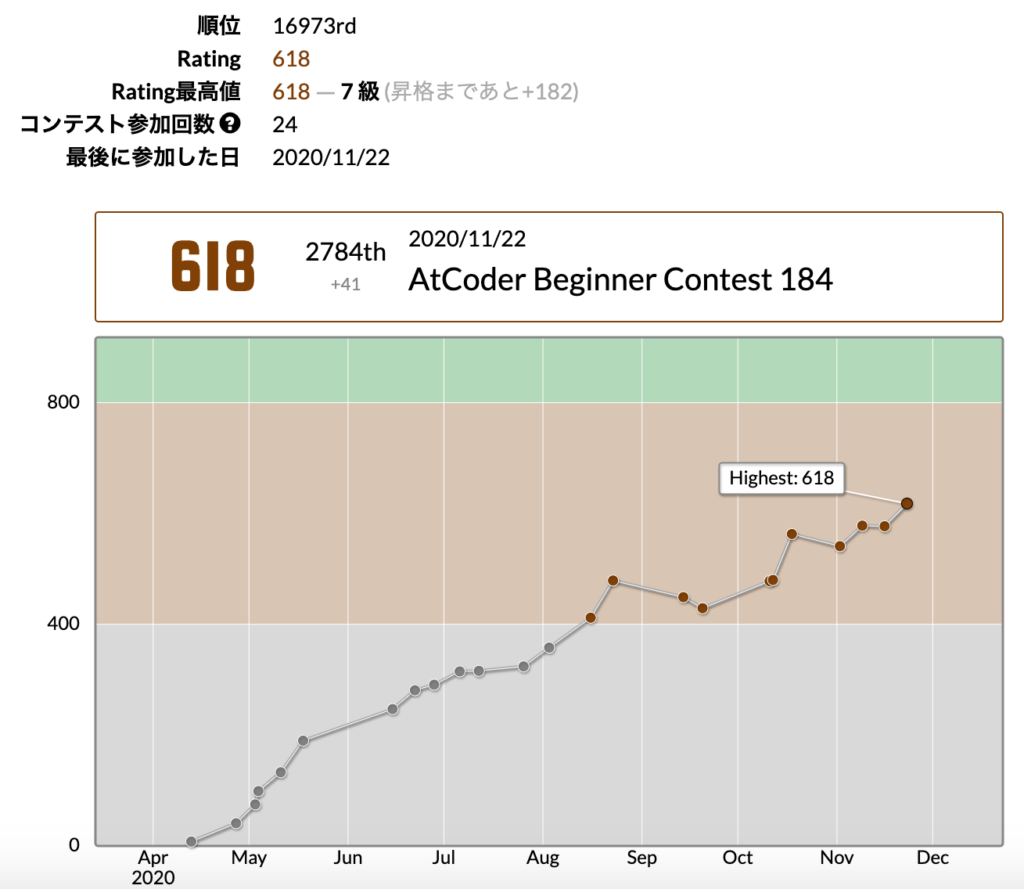
E8691 公開アカウント 13 日目 昨日の解説と今日の典型問題です グラフ理論が絡む問題は久しぶりですね 昨日と同様 入力形式 入出力例は Github を参照のこと 競プロ典型90問 T Co Jvj5ya8zp0 Twitter

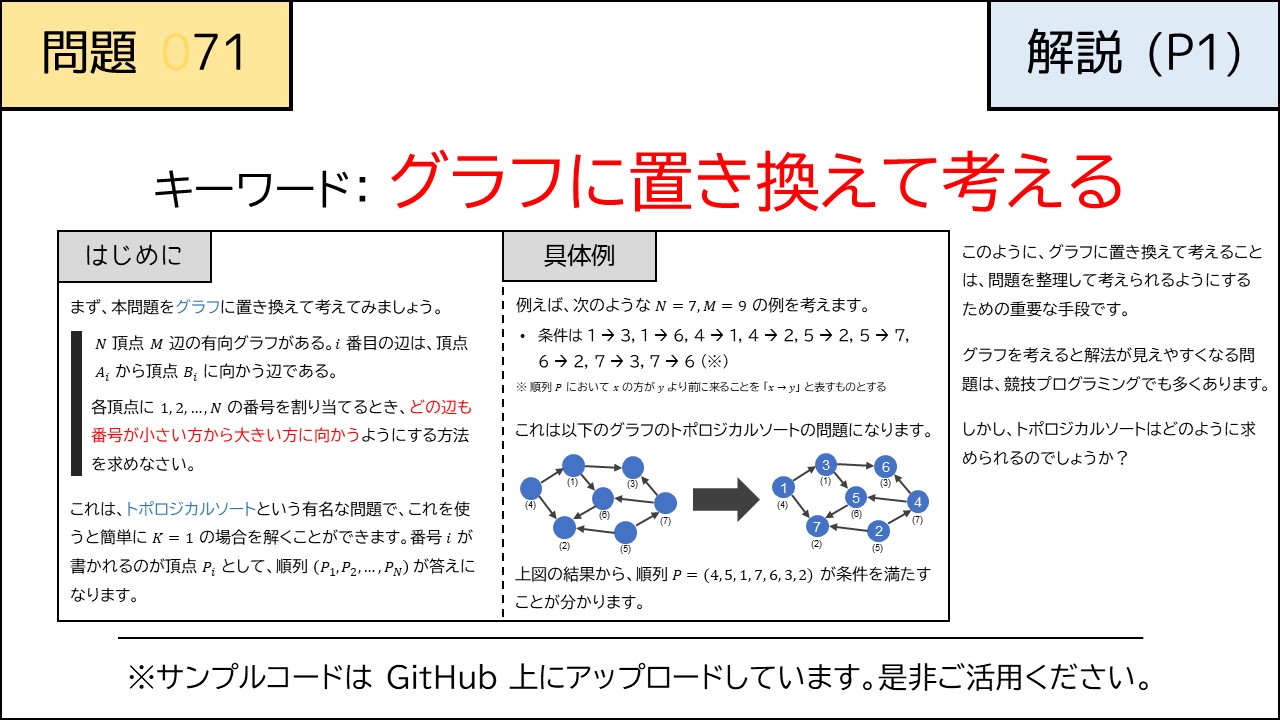
 ## 概要 競技プログラミング初級者を対象にした勉強会です。 今回はグラフデータ構造にまつわる問題に取り組んでいきます。 最初の1時間ほどでグラフデータ構造に関する基礎知識を共有します。 残りの時間でAtCoderの過去問のうちグラフにまつわる問題を解き進めていきます。 競プロでたまに出てくるけど忘れがちな定理・公式などをまとめる予定です。 （まだ下書き中） 定理 数え上げ系 行列木定理 問題例 頂点 辺のグラフの（ラベル付き）全域木はいくつありますか。 答え ラプラシアン行列の任意の余因子の行列式の 倍 ピックの定理 問題例 格子点を頂点とする

グラフ問題 競プロ

グラフ問題 競プロ- 例題2 次の比例のグラフをかきなさい。 (1) y = −2x y = − 2 x (2) y = 1 3x y = 1 3 x 基本比例のグラフの性質 の最後で見たように、比例のグラフは原点を通る直線になります。 よって、原点以外に通る点がわかれば、グラフをかくことができます。 (1)の ここまでは順調でした。 c問題 解けそうだけど、何から手をつけていいか分からず思考が停止してしましました。小学校で習った「きはじ」をしっかりと使いこなすことができれば、こんなに時間はかからなかったと思います。距離を求めたい時に、時間× 読者になる 無能が競プロやって

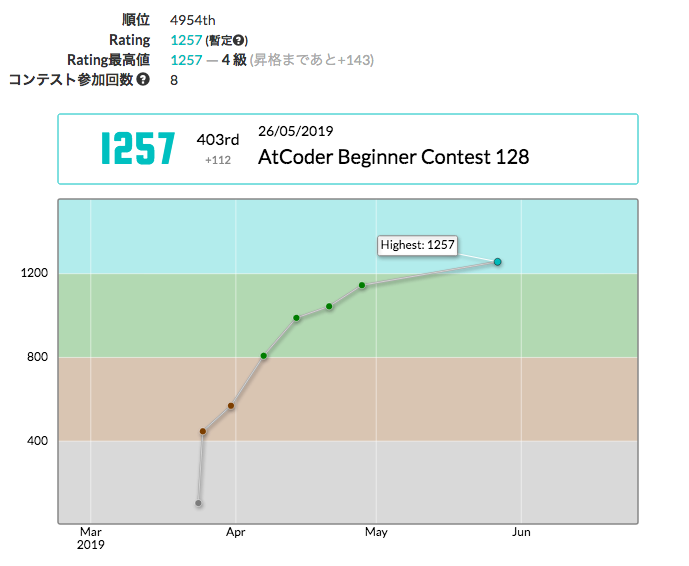
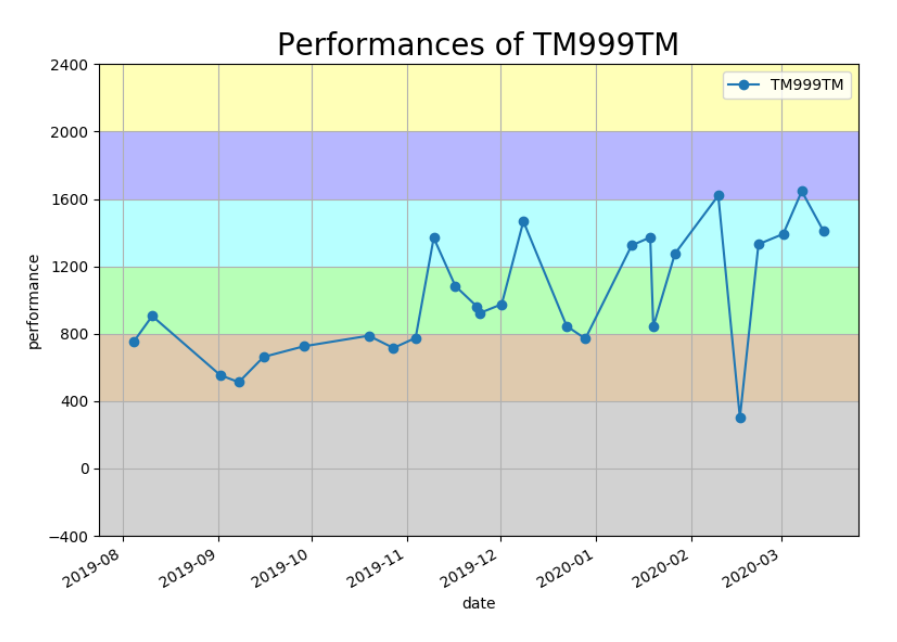
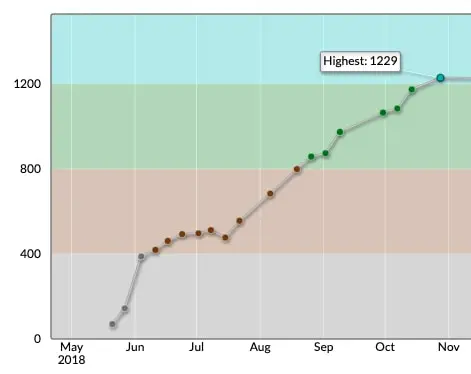
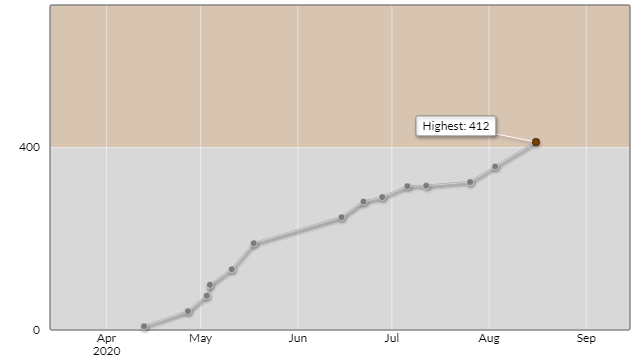
Atcoder で水色になるまでを振り返る 山傘のプログラミング勉強日記

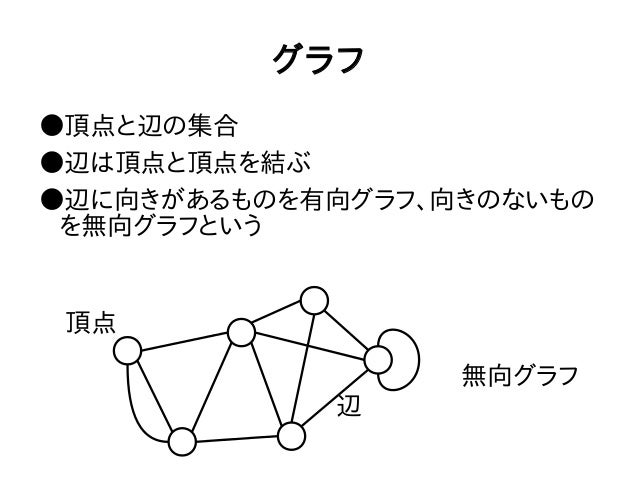
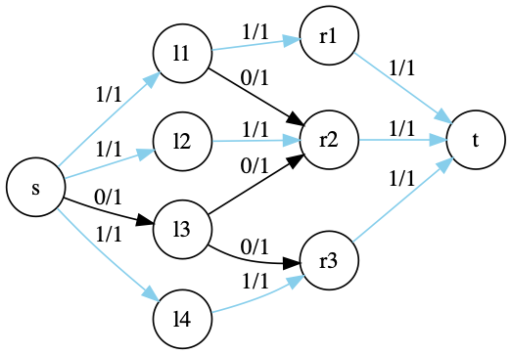
 はじめに ICPC 21 国内予選に 2 Accepted という名前のチームで出場をしていました！ 結果は，ABDE 4 完で $ 32 $ 位 の学内 $ 2 $ 位でおそらく通過となりました！ よーし．ホスト校枠もおそらく温存かな？ 去年ホスト校枠にすらひっかからず予選落ちした時は顔面ぐちゃぐちゃに 有向グラフを任意の2頂点が強連結 (互いに連結)である頂点集合を成分として分解する 強連結成分を縮約すると有向グラフがDAGになる (DPやトポロジカルソートができるようになる) 強連結成分分解を使って2SAT問題が解ける これ 小ネタ ある無向グラフの辺 問題文 N 頂点 M 辺の連結な単純無向グラフが与えられます。 グラフの頂点には、 それぞれ 1 から N までの番号が振られています。i 番目の辺は、頂点 a_i と b_i を双方向に結んでいます。 10^9 種類の色があり、各色には 1 から 10^9 までの番号が振られています。 最初、すべての頂点は色 1

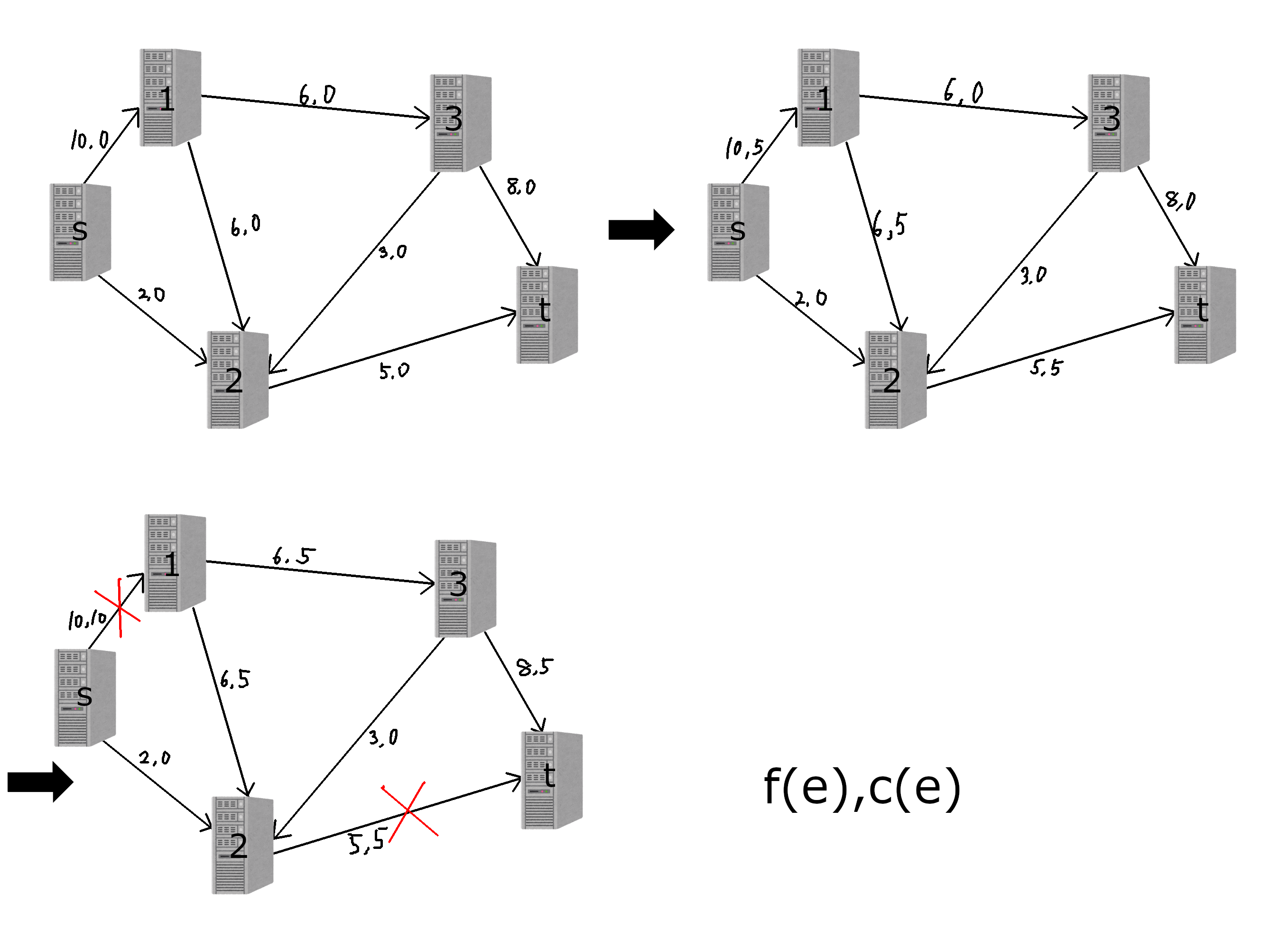
B問題が解けない人は、競プロの問題に慣れられていない可能性が高いです。先ほど紹介した AtCoder ProblemsのTrainingのEasyを解くことで競プロの問題にある程度慣れ親しめると思います。 C問題が解けない人(diffが300~600程度の問題) C問題が解けない人は、愚直に実装はできるものの、少し考え グラフ描画用のツール グラフを描画するためのツールをまとめておきます．他に知っている方は教えてくださると喜びます． 1 Graphviz DOT言語でグラフを記述して Graphviz で SVG やPDFなどに変換します．様々な描画 アルゴリズム が実装されていて 競プロについてのメモ 場合 → そのまま流せばいい 辺 の容量を1減らす → ならそのまま，それ以外なら残余グラフで押し戻す 詳しくは問題例のBox Witch のあたりに書いた 容量が負 NPhardなので難しいが変形で消せる場合もある 最小費用流 始点から終点に水を流す問題

グラフ問題 競プロのギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「グラフ問題 競プロ」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「グラフ問題 競プロ」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「グラフ問題 競プロ」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「グラフ問題 競プロ」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「グラフ問題 競プロ」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「グラフ問題 競プロ」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「グラフ問題 競プロ」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「グラフ問題 競プロ」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「グラフ問題 競プロ」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「グラフ問題 競プロ」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

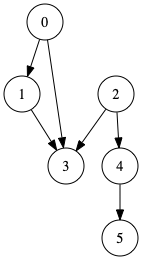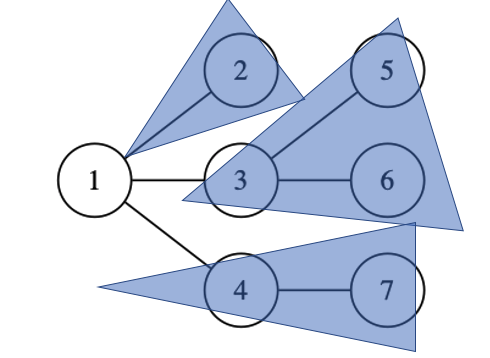「グラフ問題 競プロ」の画像ギャラリー、詳細は各画像をクリックしてください。

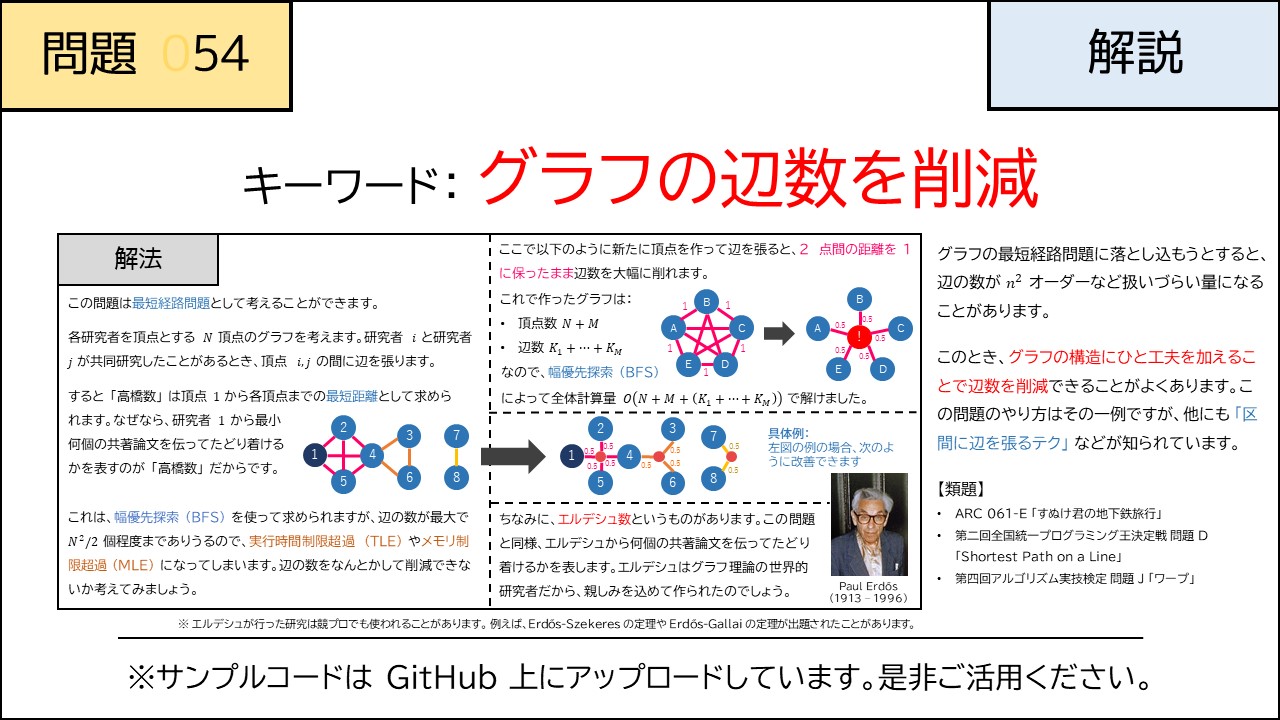
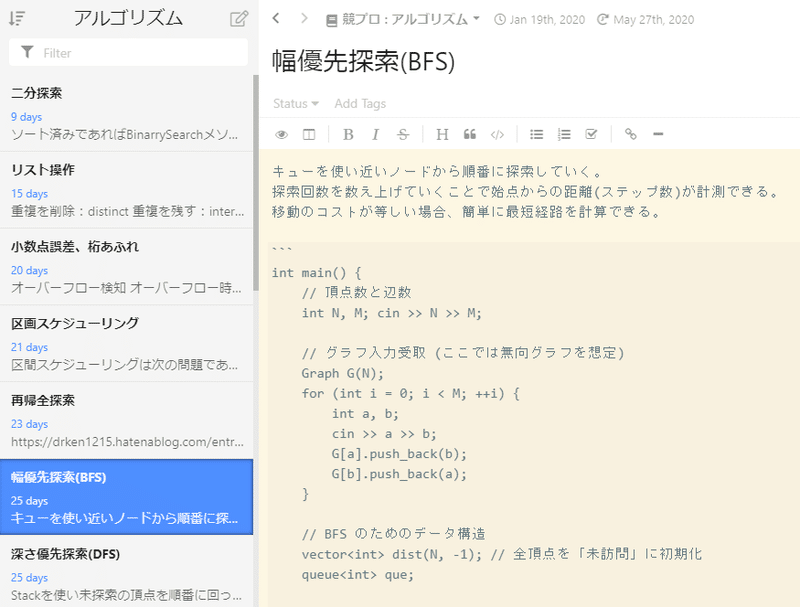
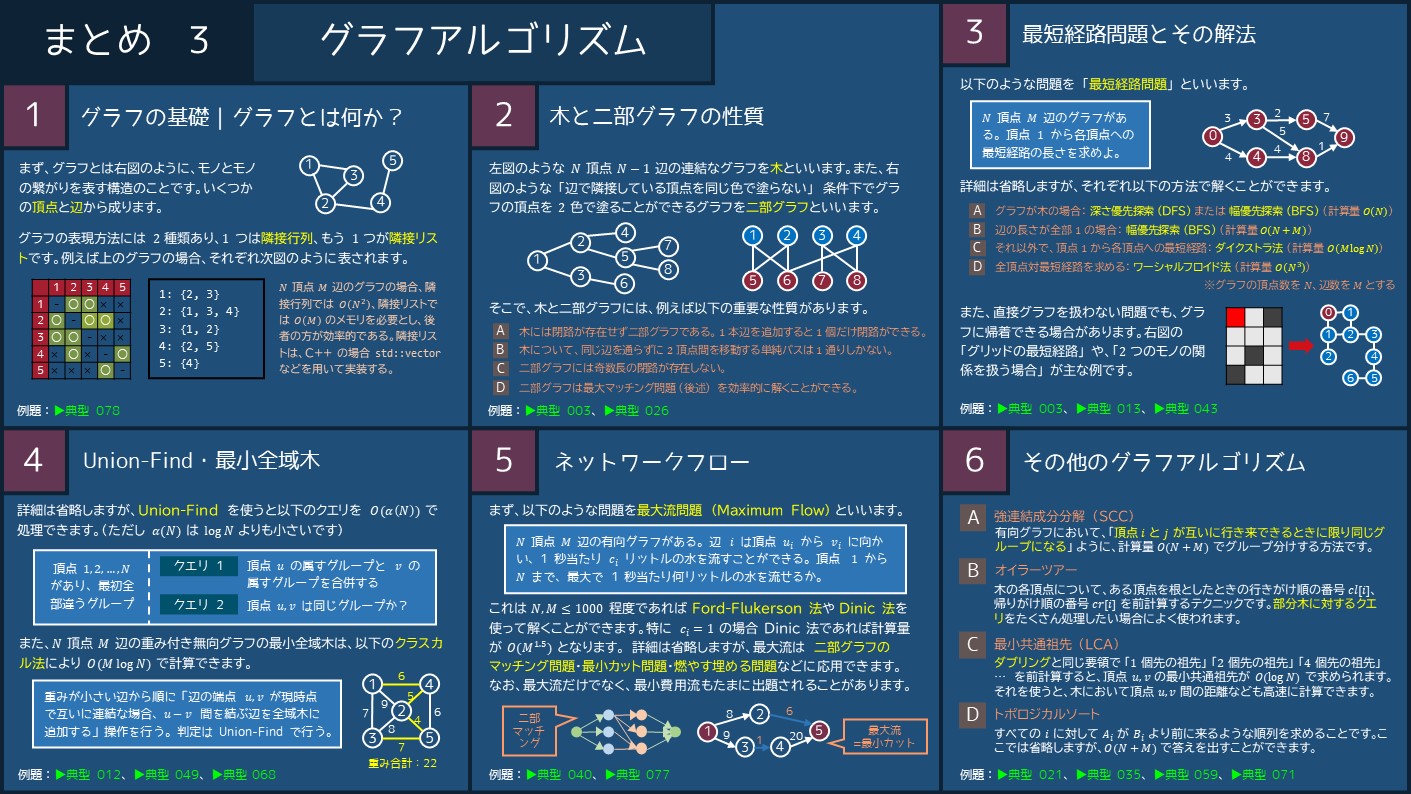
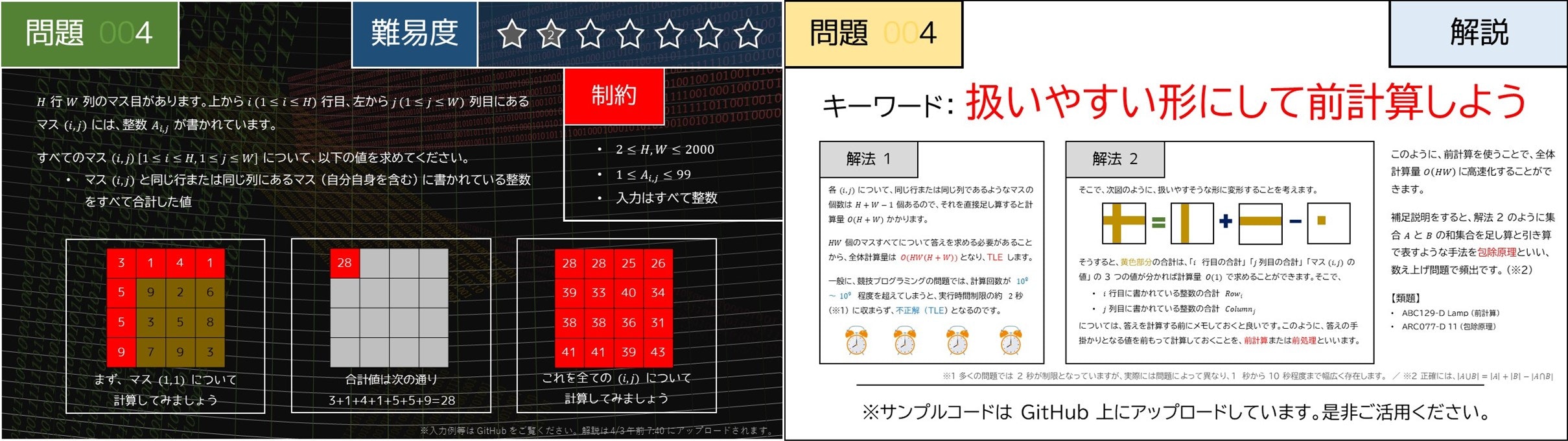
 グラフ系アルゴリズム：01BFS 競プロのアルゴリズムまとめ 今回は競技プログラミングに関する記事です。 以前、グラフのノード間の最短距離を求めるアルゴリズムとしてこちらの3つをご紹介いたしました。 グラフ系アルゴリズム：ダイクストラ法 制約 考えたこと 一般にグラフの最小頂点被覆問題は NP 読者になる けんちょんの競プロ精進記録 競プロの精進記録や小ネタを書いていきます AOJ 3168 Capture Ebichan (HUPC day1E) AOJ HUPC フロー マッチング NP困難(特殊構造なので解ける) 二部グラフ グラフ問題 前処理 最短路問題 前処理